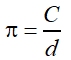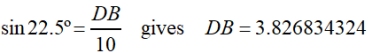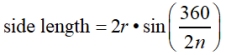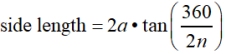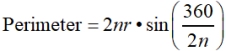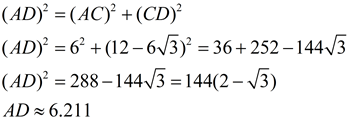Circumference of a Circle |
The perimeter of a circle is called the circumference and is the linear distance around the edge of a circle. The circumference of a circle is proportional to its diameter, d, and its radius, r, and relates to the famous mathematical constant, pi (π).
C = π • d or C = 2π • r
Circumference is from Latin meaning "carrying around".
If you "unroll" the outer edge of a circle, it will form a straight segment whose length is three diameters plus a little bit more. You will get this same result using a circle with extremely small radius length, as you will using a circle with enormously large radius length. It was the need to understand this constant length that led to the constant pi (π = 3.14159...).

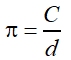 |
The number π (pi) is the ratio of a circle's circumference to its diameter.
(Multiply both sides by d to see the circumference formula, C = π • d )
|
As we have seen, the formula for the circumference of a circle
is related to the value of π, and is expressed as C = π • d = 2π • r.
But, how did the values of C and π come to be related to one another in this manner?
Let's take a look.
| Derivation (proof) of the Circumference Formula: |
The "formal" derivation of the circumference formula involves arc lengths with calculus integration, which is beyond the scope of this course. We can, however, examine the relationship between π and circumference, and take a look at Archimedes' investigation based upon geometry.
How did π become connected to circumference?
We saw in the "Types of Regular Polygons" chart that as the number of sides of a regular polygon increases, the appearance of the polygon approaches that of a circle.
The polygons in the diagram below are "regular" polygons with equal radii.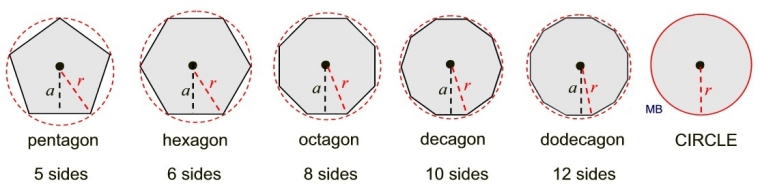
In the illustration above, as the number of sides of the polygon increases:
• the open space between the polygon and the circumscribed circle gets smaller.
• the radius, r, of each of these polygons remains the same.
• the apothem length, a, is getting longer (approaching the radius length).
• the lengths of the sides of the polygons are getting shorter (pushing closer to the circumscribed circle).
• the perimeter of the polygon is slowly increasing.
Since we are interested in "circumference", let's take a closer look at "perimeter".
If junior high school, you learned that if a regular polygon had 8 sides and you knew that
each side measured
7.7 inches, the perimeter would be 8 • 7.7, or 61.6 inches.
EASY!! But, how do you find the perimeter, if you do NOT know the length of a side?
Let's take a look.
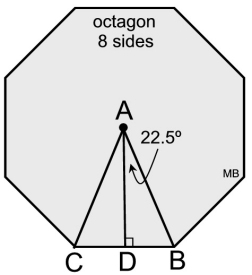
In a regular octagon (8 sides), with a given radius = 10 inches, find the perimeter.
• the central angle (∠CAB) = 360/n = 45º
(n = number of sides)
• m∠CAD = m∠BAD = 22.5º
• given radius length: AB = 10 and AC = 10
• 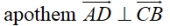 (apothem is "height" of ΔCAB). (apothem is "height" of ΔCAB).
To find the perimeter, we need to know the length of one side of the octagon, such as CB.
Using right triangle trigonometry, we can find DB.
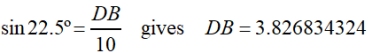
(full calculator display)
DB = ½ CB, hence CB = 7.653668648
Perimeter = 8 • CB |
regular octagon
Perimeter = 8 • 7.653668648
= 61.229 inches
(rounded to 3 decimal places) |
The process shown above is the best way to find the perimeter if given the radius, or the apothem (height).
It requires using known skills, not "fancy" formulas for regular polygons.
If we repeat the process shown above for each of our polygons of radius 10 inches,
we will get the following information:
radius of each = 10 inches
PERIMETERS of regular polygons:
pentagon (5 sides): 58.779"
hexagon (6 sides): 60.000"
octagon (8 sides): 61.229"
decagon (10 sides): 61.803"
dodecagon (12 sides): 62.117"
100-gon (100 sides): 62.822" |
rounded to
3 places
P / 2r
2.939
3.000
3.061
3.090
3.106
3.141 |
As the perimeters
of the polygons
approached the "perimeter"
of the circle,
the division of the perimeters by twice the radius approached
the value of pi, π.
Pi, π, is the value
of the circumference
of the circle
divided by twice its radius
(or diameter)
. |
| circle circumference = 62.832"
As the number of sides increased, the perimeter of the polygon approached the circumference of the circle.
|
C / 2r
3.142 |
 |
Thus, the connection between π and circumference
and the basis for the definition of circumference.
 |
The circumference of a circle is the limit of the "perimeters" of the inscribed regular polygons as the number of sides increases without bound. |
|
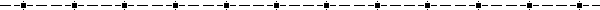
"Fancy formulas for regular polygons":
Find the length of a side of the polygon given the radius:
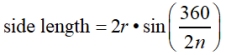
n = number of sides, r = radius |
Find the length of a side of the polygon given the apothem (height):
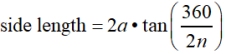
a = apothem (height) |
Find the perimeter of the polygon given the radius.
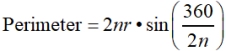 |
In each of these formulas, (360/2n) can be simplified to (180/n).
Archimedes' geometric approach to circumference and pi:
Archimedes (287 - 212 BC) was an Ancient Greek mathematician, physicist, engineer, and inventor. Archimedes first discovered that as the number of sides of a regular polygon increased, the polygon's shape approached that of a circle. This allowed him to determine the value of π, the circumference of a circle, the area of a circle, the surface area and volumes of spheres, and other mathematical concepts. Using a geometrical approach, Archimedes described how to find the relationship between the circumference of a circle and π, and how to determine the value of π.
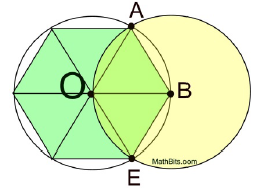 |
Archimedes Discovery:
Draw circle O. From point B, on the circle, draw another circle with center at B, and radius OB. The intersections of the two circles at A and E form equilateral triangles AOB and EOB, since they are composed of 3 congruent radii. Extend the radii forming these triangles through circle O to form the inscribed regular hexagon with 6 equilateral triangles.
|
The perimeter of the hexagon is 6 times the radius of the circle. But it can be seen that the actual circumference of the circle is "bigger" than this perimeter. Thus, the circumference of the circle must be more than 6r. [Think: In C = 2π • r, our findings show that π must be slightly bigger than 3, which we know to be true. 2π r > 6r ⇒ 2π r > 2•3r ⇒ π > 3] |
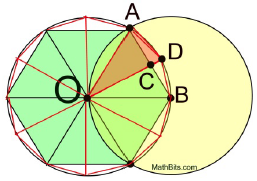 |
Attempting to get closer to the actual value of π, bisect each of the central angles of the hexagon to obtain the sides of a 12-sided figure (a dodecagon). Notice that this new polygon is getting closer to the actual circumference of the circle.
Notice that OC is the length of the altitude of the equilateral triangle (apothem), making ∠OCA a right angle, and forming ΔAOC congruent to ΔBOC. |
For ease of computation, let's say that the length of the radius, AO, in this diagram equals 12 units. We know that AB = OA (radius), so AC, which is half of AB, equals 6.
The length AD (the side of the dodecagon) can be determined by Pythagorean Thm in ΔACD.
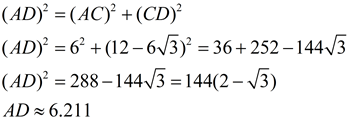 |
The perimeter of dodecagon = 12•(6.211) = 74.532. The circumference of circle O must be greater than 74.532, or greater than 6.211r. This shows π must be a little greater than 3.105.
We are getting closer to the actual value of π ! |
Archimedes saw that if you continue to increase the number of sides of the inscribed polygon, you will get closer to the actual circumference of the circle, and the solution for π will get closer to what we now know as the actual value of 3.14159...
|