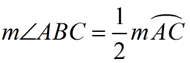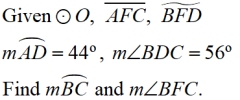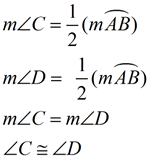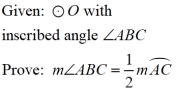Starting with this lesson, we will be investigating angles, associated with circles,
whose measurement formulas are theorems.

definition
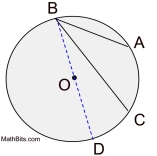
A inscribed angle of a circle is an angle whose vertex is a point on the circle and whose rays contain two other points on the circle (that is, the rays are chords).



Inscribed Angle (theorem)
The measure of an inscribed angle equals
½ the measure of its intercepted arc.

Inscribed Angle = rule2mIntercepted Arc
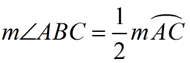angle2m
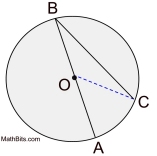
In the diagram at the right, ∠ABC is an inscribed angle with an intercepted minor arc from A to C.
angles1

m∠ABC = 41º

dividerdash

Example 1:



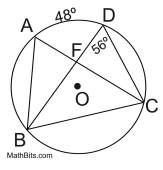
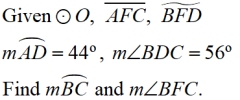
How many inscribed angles can
be seen in this diagram?
Solution:
• If the arc is 48º, then the inscribed angle, m∠ABD = 24º.

• If m∠BDC = 56º, then the minor arc from B to C has a measure of 112º. Since ∠BAC also intercepts this arc, m∠BAC = 56º.

• In ΔBAF we have angles of 56º and 24º, making m∠AFB = 100º

• Since ∠BFC is supplementary to∠AFB,
m∠BFC = 80º.

There are 8 inscribed angles.



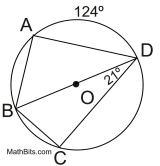
Example 2:
Solution:
• With the given diameter, there are two semicircles. ∠A and ∠C are right angles.

• m∠BDC = ½ m of the minor arc from B to C.
(21 is half of 42)

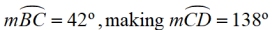
since 42 + 138 = 180 for the semicircle arc

•
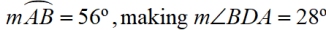For the arc: 180 - 124 = 56
For the angle: ½ of 56 = 28

dividerdash

Theorems Associated with Inscribed Angles:

theorem
An angle inscribed in a semicircle is a right angle.

(Called Thales Theorem.)

anglesemi anglesimim

 

theorem
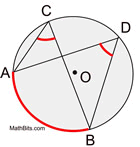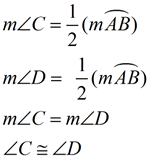In a circle, inscribed angles that intercept the same arc are congruent.		 anglesame anglesamem

 

theorem
The opposite angles in a cyclic quadrilateral are supplementary.

A quadrilateral inscribed in a circle is called a cyclic quadrilateral.

 anglesemi angcycm∠x and ∠y are supplementary

Additional Theorems related to cyclic quadrilaterals:
• A cyclic parallelogram is a rectangle.
• If a pair of opposite sides of a cyclic quadrilateral are equal in length, then the diagonals are also equal in length.
• The measure of the exterior angle of a cyclic quadrilateral is equal to the measure of the interior opposite angle.
• In a cyclic quadrilateral, the product of the diagonals equals the sum of the products of its two pairs of opposite sides.

dividerdash

 

PROOF of the theorem on measuring an inscribed angle:
 There are actually three cases for the proof of this theorem.

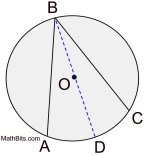
CASE 1: the center of the circle lies on one of the inscribed angle's rays (one ray is a diameter)
CASE 2: the center of the circle lies in the interior of the inscribed angle
CASE 3: the center of the circle does not lie in the interior of the inscribed angle


CASE 1:

CASE 2:

CASE 3:

• Note that CASE 1 is the primary basis for this proof, as CASE 2 and CASE 3 are based upon CASE 1.
• Note that the Exterior Angle Theorem and the Base Angles of an Isosceles Triangle Theorem are used in this proof.

divider


NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".