Information on Rational Expressions
MathBitsNotebook.com

Topical Outline | Algebra 2 Outline | MathBits' Teacher Resources

Terms of Use   Contact Person: Donna Roberts

Rational numbers are denoted by a script Q. And Q denotes rational numbers (as defined below).

Q stands for "quotient"

A rational number is a number that can be expressed as a fraction p/q where p and q are integers and q ≠ 0. It is the ratio of two integers.

You are familiar with rational numbers from your work with fractions.

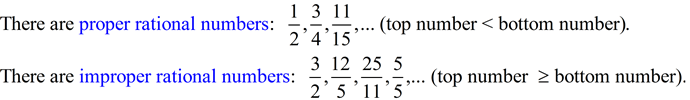
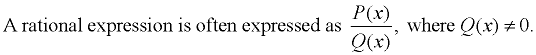
A rational expression is an expression that is the ratio of two polynomials. (where P(x) and Q(x) are polynomials)

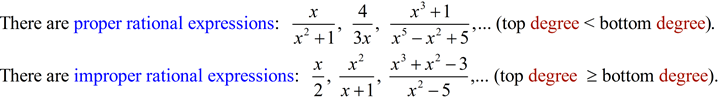
Rational expressions are algebraic fractions in which the numerator is a polynomial and the denominator is also a polynomial (usually different from the numerator). The polynomials used in creating a rational expression may contain one term (monomial), two terms (binomial), three terms (trinomial), and so on.

Rational Expressions (monomial/monomial)	Rational Expression (binomial/binomial)	Rational Expression (binomial/trinomial)

A rational expression can only equal 0, if its numerator is zero.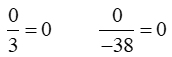

A rational expression NEVER has a zero denominator.

Expressions that are not polynomials cannot be used in the creation of rational expressions.

For example: is not a rational expression, since is not a polynomial.
This example can be referred to as a "radical expression" or an "algebraic fraction",
but not as a "rational expression".

An "algebraic fraction" is a ratio of two algebraic expressions, where the numerator and denominator
can be any polynomial or expression containing variables and constants.z
A "rational expression" is a "specific type" of algebraic fraction.

Since rational expressions represent division, we must be careful to avoid division by zero (which creates an "undefined" situation).

If a rational expression has a variable in its denominator, we must ensure that any
value (or values) substituted for that variable will not create a zero denominator.

If it is not obvious which values will cause a division by zero error in a rational expression,
set the denominator equal to zero and solve for the variable.

Values that cause zero denominators are reported in the "domain" of the expression.

The domain of a rational expression will be the set of values that can be used to replace the variable, without creating an undefined zero denominator.

Could this rational expression possibly be undefined? If so, when?		Could this rational expression possibly be undefined? If so, when?
	Obviously, when x = 1, the denominator will be zero, making the expression undefined. Domain:All Real numbers but not x = 1.		Set the denominator = 0 and solve. a2 - 4 = 0 a2 = 4
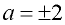For this rational expression, we must limit the x's which may be used, to avoid a division by zero error, which leaves the expression undefined. Notation: read "all x's such that x ≠ 1."		For this rational expression, we must prevent two x-values from being used in the expression. Domain: All Real numbers but not a = 2 nor a = -2.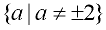
Could this rational expression possibly be undefined? If so, when?		Could this rational expression possibly be undefined? If so, when?
	Set: 8 - y = 0          8 = y Domain: All real numbers, except y = 8.		Set: x2 + x - 12 = 0 (x - 3)(x + 4) = 0 x - 3 = 0;     x = 3 x + 4 = 0;    x = -4 Domain: All real numbers, but not x = 3 and not x = -4.

When working with rational expressions,
you may see a statement indicating where the expression will be undefined.

If such information is not stated, you may be asked to supply this information
about the "domain" of the rational expression.