|
|
We saw an introduction to the concept of "end behavior" of a graph in Algebra 1.
 |
"End behavior" refers to the appearance of a graph as it is followed farther and farther in either direction (as the x-value gets very large or very small.
|
|
We have seen graphs with an arrow on either (or both) ends of the function indicating that the function continues "in the same manner" as the x-values continue to increase or decrease.
In the graph at the right, the arrow on the right end of the function tells us that as the x-values get larger and larger, the function (the y-values) will also get larger and larger. We say: "as x approaches positive infinity, f (x) approaches positive infinity." The "end behavior" is: as x → +∞, f (x)
→ +∞.
In a similar manner, the arrow on the left end of this function says, as the x-values get smaller and smaller, the function will get smaller and smaller. We say: "as x approachers negative infinity, f (x) approaches negative infinity."
The "end behavior" is": as x → -∞, f (x)
→ -∞. |
 |
In all of our discussions of "end behavior" in Algebra 1, the "ends" of the graphs approached either positive infinity or negative infinity.
So, how do we discuss "end behavior" of a graph, when one end of the graph STOPS at some endpoint, such as the case of a square root function?
RE: End behavior at an "endpoint".
We know that "end behavior" typically addresses the
behavior of a graph as the x-values approach ± infinity. So, in order to express "end behavior"
when x is approaching an endpoint, we need to amend the notation to indicate the direction x is traveling on its journey to the endpoint. This direction designation will be a superscript.
(+) means x is approaching from the right side of the endpoint (coming from the right)..
(-) means x is approaching from the left side of the endpoint (coming from the left).
Example:
as x→ 0+, f (x)
→ 0,
(as x approaches 0 from the right side, the function f (x) will approach 0) |
|
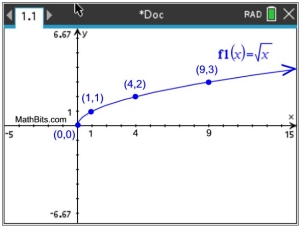
The square root function (and any even root function) has an end-point at one end of the graph.
As such, we need to amend our statement of the end behavior of the graph at that end-point.
The end behavior of the parent square root function:
as x → +∞, f (x)
→ +∞,
as x → 0+, f (x)
→ 0
The second notation tells us that there will be a stopping point on the graph. As x approaches 0 from the right,
the function graph will approach 0. |
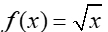 |
|
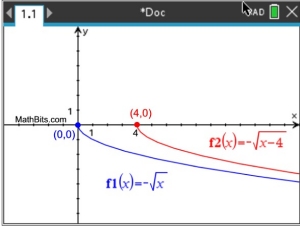
Check the end behavior of the square root function after a reflection in the x-axis, and after an added translation.
Reflection in the x-axis: 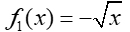
The end behavior of this negation of the square root function:
as x → +∞, f (x)
→ -∞
as x → 0+, f (x)
→ 0
Reflection in the x-axis along with a horizontal shift (translation) 4 units to the right: 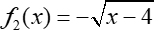
The end behavior:
as x → +∞, f (x)
→ -∞
as x → 4+, f (x)
→ 0 |
 | |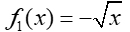
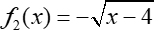
|
|
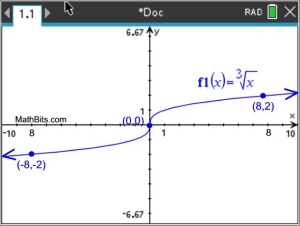
The cube root function (and any odd root function) will display the standard end behavior of approaching ± infinity.
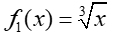
The end behavior of this cube root function:
as x→ +∞, f (x)
→ +∞
as x → -∞, f (x)
→ -∞ |
|
|
For
calculator help with graphing
radical functions.
click here. |
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|