In your study of mathematics, you have encountered "exponents" at several past grade levels and in many different types of application problems. Let's review some aspects about exponents that you may, or may not, already know.
Exponents may also be referred to as "powers" or "indices".
In other countries, such as the United Kingdom, Australia, and India, "exponents" are referred to as "orders". These countries write an equivalent form of PEMDAS as BODMAS (Brackets, Orders, Division, Multiplication Addition, Subtraction).
There are two exponents that have been given a "specific name".
• "Squared" refers to raising a quantity to the second power.
• "Cubed" refers to raising a quantity to the third power.
Exponents are simply a shorthand for repeated multiplication of the same quantity,
23 = 2 x 2 x 2
1.46 = 1.4 x 1.4 x 1.4 x 1.4 x 1.4 x 1.4
816 = 8 x 8 x 8 x 8 x 8 x 8 x 8 x 8 x 8 x 8 x 8 x 8 x 8 x 8 x 8 x 8 (Definitely need exponents!)
The word "Power" and the word "Exponent" |
When working with numerical computations, the terms "power" and "exponent"
are basically interchangeable.
46 is "4 raised to the 6th power",
46 is "4 with an exponent of 6".
Some textbooks, however, may point out a very minor difference between these terms. They state the difference is that "exponent" refers only to the number of times (6), that the given base number (4) is being multiplied by itself, while "power" refers to the "entire expression" (the base and the exponent together, 46 ). Yes, math can be picky at times!
"Power" Expression VS "Exponential" Expression |
When you enter the realm of "algebraic expressions and functions", the word "exponent" is morphed into the word "exponential" and the words "power" and "exponential" take on different meanings.
In a "power expression or function", the variable is located in the base, and the exponent is constant.
Examples: 3x2 or f (x) = 3x2 [function: f (x) = axn]
In an "exponential expression or function", the variable is the exponent, and the base is constant.
Examples: 2x or f (x) = 2x [function: f (x) = abx ; (b > 0, b ≠1)]
Work with "exponentials" will continue under Exponents/Logarithms.
Why is any non-zero number raised to the power of 0 always equal to 1.
The answer to this question is based upon the division property for exponents. When dividing exponents with the same base, the exponents are subtracted.
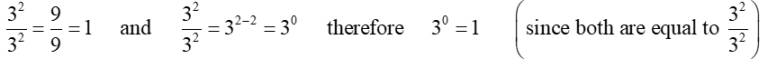
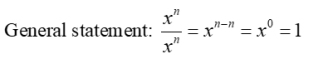
So, why is the number zero raised to the power of 0 considered undefined?
If it is assumed that 00 = 1, in keeping with our first question, then serious mathematical inconsistencies will be encountered.
In
Algebra 2, we will take a look at a simple example using two graphs that will demonstrate a mathematical inconsistency when dealing with 00. Consider what would happen if the following graphs were graphed as shown below. (focus on x = 0)
In the graph at the right, x cannot be negative since it will place 0 in the denominator, which will be undefined.
Each graph appears to be establishing a "pattern" for the solutions to the equations. Unfortunately, each graph's pattern implies a different possible value for 00.
In the first graph's pattern, if we consider any number (not zero) raised to the zero power to be one, then shouldn't zero raised to the zero power fall into that pattern and also be one?
In the second graph's pattern, if we consider any positive number raised to the zero power to be zero, then shouldn't zero raised to the zero power fall into that pattern and also be zero?
Mathematically speaking, it is NOT possible for 00 to be equal to BOTH 1 and 0. Consequently, 00 is described as being undefined. The actual graphs for the functions shown above will require an "open circle" placed at x = 0 to designate a break in the graph.
In Calculus, you will learn a more detailed explanation of this answer based upon an investigation with limits.
