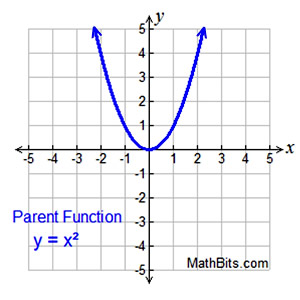
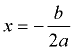Shape: Parabola Shape: Parabola
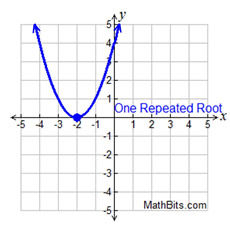
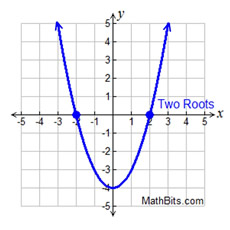
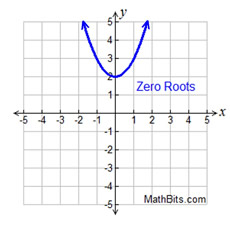
Quadratic Function - Possible Real Roots and Complex Roots:
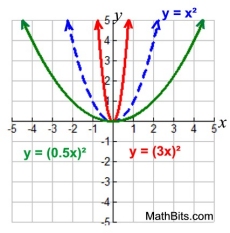
Maximum/Minimum: Finding the "turning point" (vertex) will locate the maximum or minimum point. The intervals of increasing/decreasing are also determined by the vertex. Quadratic Function - Transformation Examples:
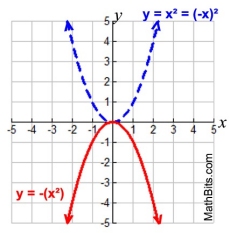
Remember: for y = ax2 + bx + c, negative "a" opens down.
Topical Outline | Algebra 2 Outline | MathBitsNotebook.com | MathBits' Teacher Resources
|