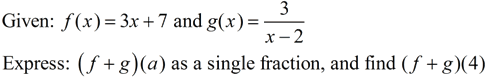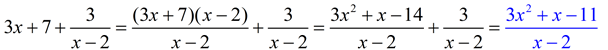|
Functions can be added, subtracted, multiplied and divided. Such procedures are referred to as "operations of functions" or "algebra of functions". These arithmetic procedures can be performed on two functions when the functions have the same domains (and no division by zero occurs).
|
Domains
 |
|
The domain for each of these new functions will be the
intersection (∩) of the domains
of functions f (x) and g(x). Basically speaking, you need to find where the domains overlap.
There is an additional stipulation for the domain of (f / g)(x) which states that g(x) cannot equal 0, to avoid a division by zero problem.
Examples:
1. Given f (x) = 5x + 1 and g (x) = 3x - 2.
Express (f + g)(x); (f - g)(x); (f • g)(x); (f / g)(x)
State the domain of each.
|
Solution:
(f + g)(x) = f (x) + g(x) = (5x + 1) + (3x - 2) = 8x - 1
Domain: D(f ) = Reals and D(g) = Reals, so D(f + g) = D(f ) ∩ D(g) = Reals
(f - g)(x) = f (x) - g(x) = (5x + 1) - (3x - 2) = 2x + 3
Domain: D(f ) = Reals and D(g) = Reals, so D(f + g) = D(f ) ∩ D(g) = Reals
(f • g)(x) = f (x) • g(x) = (5x + 1) • (3x - 2) = 15x2 - 7x - 2
Domain: D(f ) = Reals and D(g) = Reals, so D(f + g) = D(f ) ∩ D(g) = Reals

Domain: D(f ) = Reals and D(g) = Reals, but D(f + g) = D(f ) ∩ D(g) = Reals, but not x = 2/3
(The x = 2/3 creates a zero denominator problem with division by g(x).)
2. 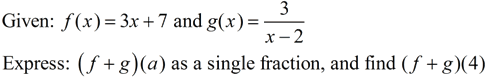 |
Solution:
(f + g)(x) = f (x) + g(x) = 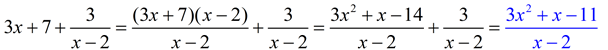
(f + g)(4) = f (4) + g(4) = 19 + 3/2 = 20½
FYI: D(f + g)(x) = D(f) ∩ D(g) = (Reals) ∩ (Reals - {2}) = Reals - {2}
3. Given the tables shown below:
x |
2 |
4 |
6 |
8 |
f (x) |
23 |
16 |
30 |
26 |
|
x |
2 |
4 |
6 |
8 |
g(x) |
28 |
32 |
-14 |
-22 |
|
Express (f + g)(6); (f - g)(8); (f • g)(2); (f / g)(4)
|
Solution:
(f + g)(6) = f (6) + g(6) = 30 + (-14) = 16
(f - g)(8) = f (8) - g(8) = 26 - (-22) = 48
(f • g)(2) = f (2) • g(2) = 23 • 28 = 644
(f / g)(4) = f (4) / g(4) = 16 / 32 = ½
FYI: The domains for all of these functions will be {2, 4, 6, 8}. There are no division by zero problems since neither f (x) nor g(x) ever equal 0.
4. Given the graphs shown below on the interval [-4,4], with line segments connecting certain designated points whose x and y values are integers:
 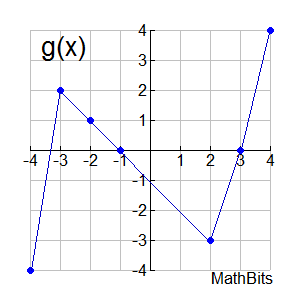
Express (f + g)( -2); (f - g)(4); (f • g)(-4); (f / g)(2)
|
Solution:
(f + g)(-2) = f (-2) + g(-2) = 1 + 1 = 2
(f - g)(4) = f (4) - g(4) = -3 - (4) = -7
(f • g)(-4) = f (-4) • g(-4) = 3 • (-4) = -12
(f / g)(2) = f (2) / g(2) = 0 / (-3) = 0
FYI: The domains for the first three of these functions will be the interval [-4, 4]. The domain for the last function ( (f / g)(x) ) will be [-4,4] - {-10/3 , -1, 3}. There are three trouble spots (x-intercepts) where g(x) returns a zero answer causing division by zero. To find the x-intercept between -4 and -3, we need the equation of the segments connecting the points (-4,4) and (-3,2).
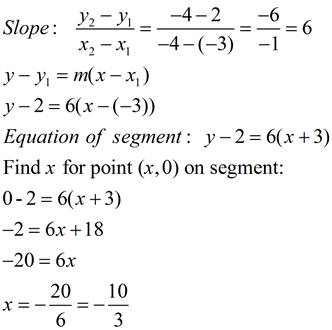
|
For calculator help with
algebra of functions
click here. |
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|