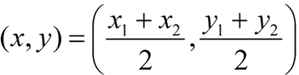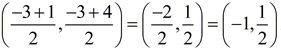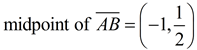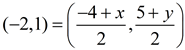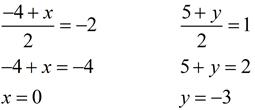|
|
A midpoint of a segment is the point on that line segment that divides (partitions) the segment into two congruent segments. |
|
The midpoint of a segment is the point on the segment that is equidistant from the endpoints.
The midpoint is the point on the segment halfway between the endpoints.
It may be the case that the midpoint of a segment can be found simply by counting.
If the segment is horizontal or vertical, you can find the midpoint by dividing the length of the segment by 2 and counting that value from either of the endpoints.
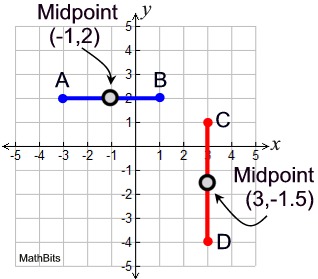
Example 1: Given the graph at the right, find the midpoint of 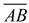 and of and of 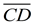 . .
AB = 4 units (by counting). The midpoint is 2 units from either endpoint. This midpoint is (-1,2).
CD = 5 units (by counting). The midpoint is 2.5 units from either endpoint. This midpoint is (3,-1.5). |
|
If the segment lies diagonally across the coordinate axes, more thought will be needed to find the midpoint.
When you are finding the coordinates of the midpoint of a segment, you are actually finding the average (mean) of the x-coordinates and the average (mean) of the y-coordinates.
The midpoint formula works for ALL line segments: vertical, horizontal or diagonal.
The midpoint formula finds an ordered pair. |
Midpoint Formula:
The midpoint (x,y) of a segment with endpoints (x1, y1) and (x2, y2) has coordinates 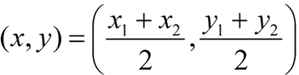 |
|
Example 2: Find the midpoint of segment 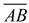 , where A(-3,-3) and B(1,4). , where A(-3,-3) and B(1,4).
Using the midpoint formula, we have
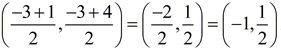
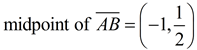
Note: Fractional answers should be left as fractions or written as decimals if terminating. Do not round these midpoint coordinates, unless told to do so. |
|
|
Example 3: Given M is the midpoint of 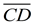 , as shown, find the coordinates of point D. , as shown, find the coordinates of point D.
By examining the graph, we can see approximately where point D will be located. When you solve for the coordinates of D, be sure they match with your approximation of point D.
Substitute M(-2,1), C(-4,5) and D(x,y) into the midpoint formula: 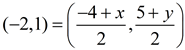
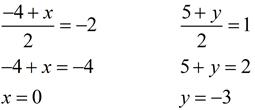
|
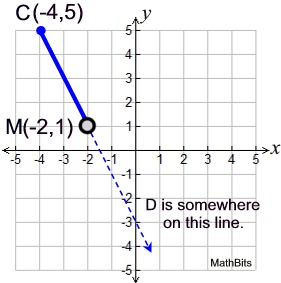
Midpoint (x,y) = (0,-3)
|
|
Method 3: Slope and Congruent Δs |
In questions such as Example 3, you may be able to find the missing endpoint by using slope and congruent triangles.
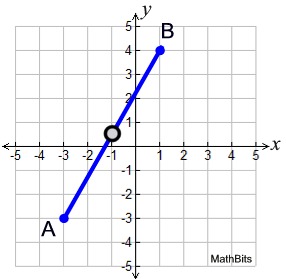
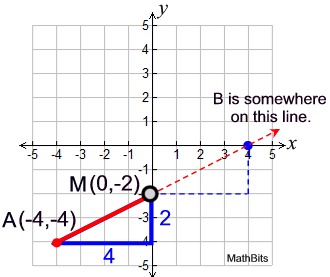
Example 4: Given M is the midpoint of 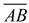 , as shown, find the coordinates of point B. , as shown, find the coordinates of point B.
If the midpoint and the endpoint coordinates are integer values (making them easy to locate), you can build congruent triangles to find the missing endpoint. We know that 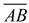 is a straight line segment whose slope (rate of change) will be constant along the segment. is a straight line segment whose slope (rate of change) will be constant along the segment.
The slope between points A and M runs 4 units to the right and 2 units up. By repeating this slope from point M (4 units right and two units up), we will find the missing endpoint B (4,0). |
|
The two triangles formed by the run of 4 and the rise of 2 each contain a right angle and are congruent by Side-Angle-Side. Since the congruent triangles have congruent hypotenuses, we know AM = MB, which verifies that M is the midpoint of 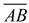 .
This approach is harder to implement when the coordinates are fractional. If you are dealing with fractional coordinates, use the midpoint formula.
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|