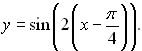|
In Algebra 1, the discussion of functional transformations included vertical and horizontal translations. Such translations also occur when dealing with trigonometric functions, with a horizontal translation, or horizontal shift, being one of the most prominent transformations.
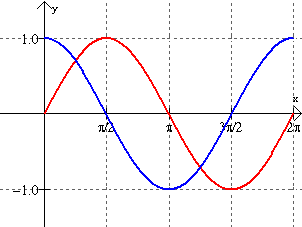
The graphs of sine and cosine are the same when sine is shifted left by 90º or 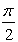 radians. Such a shifting is referred to as a horizontal shift. radians. Such a shifting is referred to as a horizontal shift.
|
shift sine to the left
to create cosine |
|
shift cosine to the
right to create sine |
|
y = cos(x); y = sin(x)
|
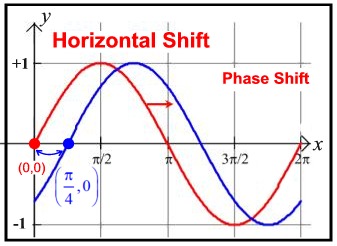
| Horizontal Shift and Phase Shift |
If the horizontal shift is positive, the shifting moves to the right. If the horizontal shift is negative, the shifting moves to the left. |
From the sinusoidal equation,
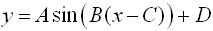
the horizontal shift is obtained by determining the change being made to the x-value.
The horizontal shift is C.
In mathematics, a horizontal shift may also be referred to as a phase shift.*(see page end)
The easiest way to determine horizontal shift is to determine by how many units the "starting point" (0,0) of a standard sine curve, y = sin( x), has moved to the right or left.
|
|
Horizontal shifts can be applied to all trigonometric functions.
 |
So, if a horizontal shift is positive when the shifting moves to the right,
why does the equation look like the shift is negative? |
|
Why does 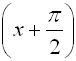 move left and move left and 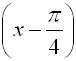 move right? move right?
Doesn't "+" mean right??? What's happening here??? |
|
When trying to determine the left/right direction of a horizontal shift, you must remember the original form of a sinusoidal equation: y = Asin(B(x - C)) + D. (Notice the subtraction of C.)
The horizontal shift is determined by the original value of C.
|
This expression is really 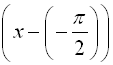 where the value
of C is negative and the shift is to the left. |
|
|
In this expression the value of C is positive and the shift is to the right. |
|
Another |
 |
* Note: Use of the phrase "phase shift":
When used in mathematics, a "phase shift" refers to the "horizontal shift" of a trigonometric graph. While mathematics textbooks may use different formulas to represent sinusoidal graphs, "phase shift" will still refer to the horizontal translation of the graph. Consider the mathematical use of the following sinusoidal formulas:
y = Asin(B(x - C)) + D
horizontal shift = C
phase shift = C |
versus |
y = Asin(Bx - C) + D
horizontal shift = C / B
phase shift = C / B
|
To add to the confusion, different disciplines (such as physics and electrical engineering) define "phase shift" in slightly different ways, and may differentiate between "phase shift" and "horizontal shift". Consider the following:
Note these different interpretations of "phase shift".
C ≠ c |
|
(Math) f (x) = A sin(B(x - C)) where C = horizontal shift |
| |
(Physics) g(x) = a sin (bx - c) where c = phase shift (but not horizontal shift c/b)
(Under this interpretation, the C in the math formula, shown above, would only represent "phase shift" when B = 1.)
|
Refer to your textbook, or your instructor, as to what definition you need to use for "phase shift",
when that phrase is being used.
To avoid confusion, this web site is using the term "horizontal shift".
It is also using the equation y = A sin(B(x - C)) + D because
it resembles previously seen transformational forms such as f (x) = a sin [b(x - h)] + k..
|
How to use your graphing calculator for graphing trig functions.
click here. |
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|

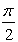 radians. Such a shifting is referred to as a
radians. Such a shifting is referred to as a 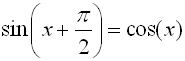
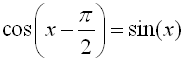

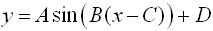
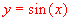
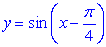


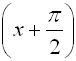 move left and
move left and 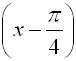 move right?
move right?
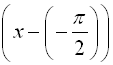 where the value
where the value 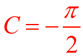
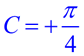
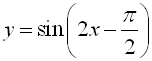 ?
?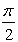 ,
, 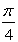 , because the equation is actually
, because the equation is actually