You saw the numerical concept of "complex fractions" in Junior Math Grade 7.
It's time, now, to place an algebraic twist on these fractions.
In so doing, we will be working with rational expressions.
This work with complex fractions will be beneficial to
understanding and solving equations that involve rational functions.
A complex fraction is a fraction in which the numerator, denominator, or both, also contain fractions.
If the complex fraction contains a variable,
it is called a complex rational expression. |
|
Examples of complex fractions:
It should be noted that the word "complex" in "Complex Fraction" means multifaceted or difficult.
It does not imply a connection to "Complex Numbers" (numbers containing an i ).
|
= |
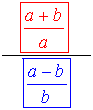 |
numerator of complex fraction
main fraction bar
denominator of complex fraction |
|
|
Complex fractions should be simplified. It is often too confusing to leave an answer in this complex format. |
|
Always remember that the fraction bar means "divided by". |
All complex fractions can be re-written as division problems.
Interpret the main fraction bar to mean "divided by".
There are two methods that can be used to simplify complex fractions.
To simplify a complex fraction means to write the expression
without
a fraction in its numerator and/or its denominator. |
Method 1: Simplify complex fractions by using division (from the fraction bar).
Method 2: Simplify complex fractions by multiplying by a common denominator.
Let's see how the 5 examples at the top of the page can be simplified using these two methods.
Method 1: Simplify complex fractions by using division.
This first method is the simplest to remember. You simply interpret the main fraction bar to mean "divided by" and then follow the rules you know for division of fractions. Life will be easier if you convert both the top fraction and the bottom fraction into "single" fractions (if needed) before dividing.
• Create one single fraction in the numerator (if necessary).
• Create one single fraction in the denominator (if necessary).
• Remember the main fraction bar means "divide". Rewrite the fraction using the ÷ symbol.
• Follow the normal rules for dividing fractions: invert the second term (the denominator of the complex fraction) and multiply by the numerator of the complex fraction.
• Simplify whenever possible.
If you are asked to state restrictions (un-usable x-values) for the complex fraction, this first method will be more advantageous as it requires converting the complex fraction's denominator into a single fraction. The top of this denominator fraction, when flipped, will become a denominator which cannot equal zero.
|
1. 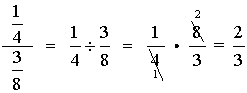 |
Remember, when dividing fractions, invert (flip over, take reciprocal of ) the second fraction and multiply.
Reduce the final answer if needed (or reduce as you multiply). |
2. 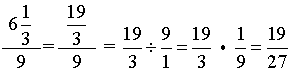
|
Remember that a mixed number should be converted to an improper fraction (heavier on top) before simplifying. |
3. 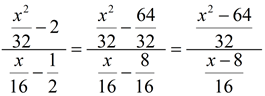
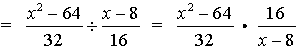
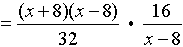
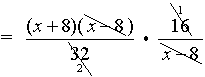
= 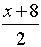 |
Remember to change the numerator and denominator to single fractions by creating a common denominator. The least common denominator for the terms in this numerator is 32. The least common denominator for the terms in this denominator is 16. Note: the two common denominators used to create the single fractions may, or may not, be the same value. Most often they are NOT the same value.)
Remember to invert the second fraction and multiply.
Remember it may be necessary to factor to reduce a fraction.
Be sure that your final answer is in simplest reduced form.
Restrictions: x ≠ 8
The original complex fraction has a restriction of x ≠ 8. Notice now the inverted denominator fraction also has a restriction of x ≠ 8. |
4. 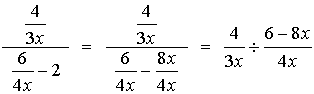
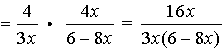
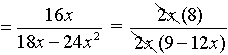
= 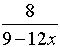 = = 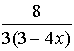 |
Remember in this problem, to change the denominator to a single fraction before you start to simplify. The least common denominator for the bottom is 4x.
Remember that after you invert the second fraction, you need to multiply. Distribute when you multiply the denominators (multiply each term by 3x).
Remember to factor the top and the bottom to simplify the answer.
Restrictions: x ≠0, ¾
The top and bottom of the original fraction cannot allow x = 0 or x = ¾. Notice how the inverted denominator fraction also needs x ≠¾ when solving (6 - 8x) = 0. |
5. 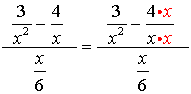
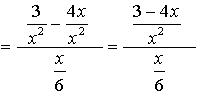
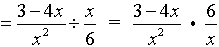
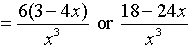 |
Remember, in this problem, to change the numerator to a single fraction before you start to simplify. The least common denominator for this numerator is x2. (The second term in the numerator will need to be multiplied by x/x to create the needed denominator.)
Remember to combine the terms in the numerator to form a single fraction in the numerator of this problem.
Remember, after you invert the second fraction, to multiply.
Express the final answer.
(When removing the parentheses in the top, be sure to distribute the 6 ... multiply each term by the 6.)
Restrictions: x ≠0
|
Method 2: Simplify complex fractions by multiplying by a common denominator.
In this method, EVERY term gets multiplied by the common denominator of all of the terms.
• Find the least common denominator (LCD) for all fractions appearing within the complex fraction.
• Multiply both the numerator and the denominator of the complex fraction by this LCD.
• Simplify whenever possible.
|
1. 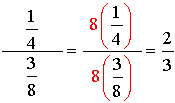
|
The least common denominator for the entire problem is 8.
Multiply the top and bottom by 8. |
2.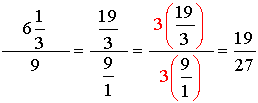 |
The mixed number needs to be changed to an improper fraction before starting Method 2. Remember that the unseen denominator for 9 is 1. The least common denominator for the ENTIRE problem is 3. Multiply the top and the bottom by 3. |
3. 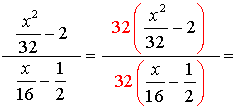
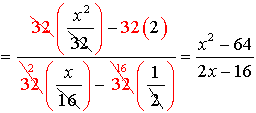
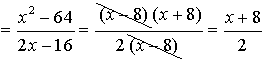 |
The least common denominator for the ENTIRE problem is 32. Multiply the top and the bottom by 32.
Be careful to distribute the 32 through the parentheses.
Now simplify by factoring the top and the bottom. Express the final answer.
Restrictions: x ≠ 8
The numerator of the bottom single fraction will become a denominator when flipped, thus it cannot equal zero.
|
4.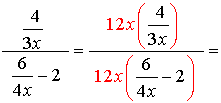
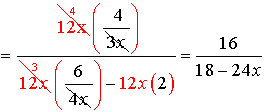
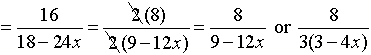
|
The least common denominator for the ENTIRE problem is 12x. Multiply the top and the bottom by 12x.
Be careful to distribute the 12x through the parentheses.
Now simplify by factoring the top and the bottom.
Restrictions: x ≠0, ¾
The top and bottom of the original fraction cannot allow x = 0 or ¾, and the flipped denominator (6 - 8x) cannot equal zero. |
5. 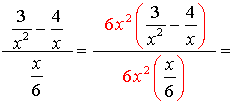
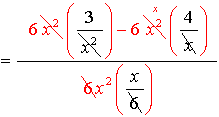
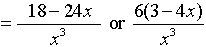 |
The least common denominator for the ENTIRE problem is 6x2. Multiply the top and the bottom by 6x2.
Be careful to distribute the 6x2 through the parentheses
Write the final answer.
Restrictions: x ≠0 |
 |
Don't let these fractions
scare you!
Just work carefully and
show your work as you progress
through the problem. |
|
|