A parabola is a conic section. It is a slice of a right cone parallel to one side (a generating line) of the cone. Parabolas and circles are quadratic relations since their equations deal with powers of two. Unlike the circle where both x and y are squared, the parabola has either x squared or y squared, but not both. You have worked with parabolas in the past when you graphed quadratic equations. We will now be investigating the conic form of the parabolic equation to learn more about the parabola's graph.
|
A parabola is defined as the set (locus) of points that are equidistant from both the directrix (a fixed straight line) and the focus (a fixed point). |
|
This definition may be hard to visualize.
Let's take a look.
For ANY point on a parabola, the distance from that point to the focus is the same as the distance from that point to the directrix. (Looks like hairy spider legs!)
Notice that the "distance" being measured to the directrix is always the shortest distance (the perpendicular distance).
The specific distance from the vertex (the turning point of the parabola) to the focus is traditionally labeled "p". Thus, the distance from the vertex to the directrix is also "p". |
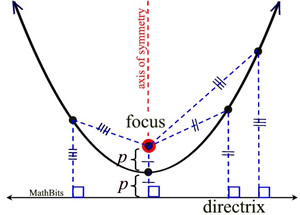
The focus is a point which lies "inside" the parabola on the axis of symmetry. The directrix is a line that is ⊥ to the axis of symmetry and lies "outside" the parabola (not intersecting with the parabola). |
Conic Equations of Parabolas: |
 You recognize the equation of a parabola as being y = x2 or
y = ax2 + bx + c from your study of quadratics. And, of course, these remain popular equation forms of a parabola. But, if we examine a parabola in relation to its focal point (focus) and directrix, we can determine more information about the parabola. We are now going to look more closely at the coefficient of the x2 term to see what additional information it can tell us about the graph of the parabola. Keep in mind that all information you already know about parabolas remains true!
 Parabola with Vertex at Origin (0,0) Parabola with Vertex at Origin (0,0)
(axis of symmetry parallel to the y-axis)
Conic Forms of Parabola Equations:
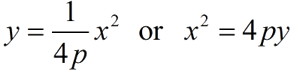
with the vertex at (0,0),
focus at (0, p) and directrix y = -p |
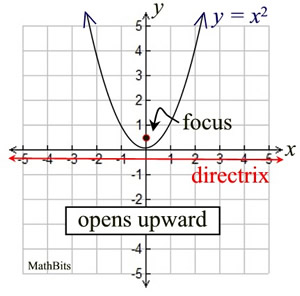
In the example at the right, the coefficient of x² is 1, so 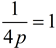 , making p = ¼. , making p = ¼.
The vertex is (0,0), the focus is (0,¼), and the directrix is y = -¼.
|
 The distance from the vertex The distance from the vertex
(in this case the origin) to the
focus is traditionally labeled as "p". |
|
The leading coefficient in y = ax2 + bx + c is labeled "a".
When examining the coefficient of
x2, we are examining a.
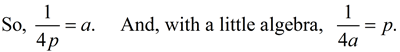 p is the distance from the vertex to the focus.
p is the distance from the vertex to the focus.
|
|
 You remember the vertex form of a parabola as being y = a(x - h)2 + k where (h, k) is the vertex of the parabola. If we let the coefficient of x2 (or a) = You remember the vertex form of a parabola as being y = a(x - h)2 + k where (h, k) is the vertex of the parabola. If we let the coefficient of x2 (or a) = 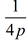 and perform some algebraic maneuvering, we can get the next equation. and perform some algebraic maneuvering, we can get the next equation.
 Parabola with Vertex at (h, k) Parabola with Vertex at (h, k)
(axis of symmetry parallel to the y-axis)
(Known as "standard form".)
Conic Form of Parabola Equation:
(x - h)2 = 4p(y - k)
with the vertex at (h, k), the focus
at (h, k+p) and the directrix
y = k - p |
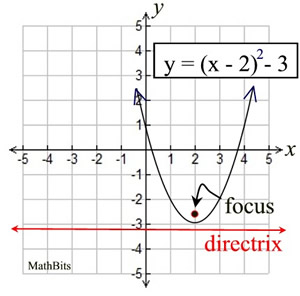
Since the example at the right is a translation of
the previous graph, the relationship between the parabola and its focus and directrix remains the same (p = ¼). So with a vertex of (2,-3), we have:
(x - 2)2 = 4(¼) (y - (-3))
(x - 2)2 = y + 3
The focus is at (2,-3+¼) or (2,-2¾) and
the directrix is y = -3-¼ or y = -3¼ |
 This "new" equation is just another form
This "new" equation is just another form
of the old "vertex form" of a parabola.
OLD: y = (x - 2)² - 3
NEW: (x - 2)² = y + 3
|
S O M E T H I N G N E W ! ! ! |
Up to this point, all of your parabolas have been either opening upward or opening downward, depending upon whether the leading coefficient was positive or negative respectively. The axis of symmetry of those parabolas is parallel to the y-axis. We will now be looking at a parabola that opens to the right or to the left ("sideways"), with its axis of symmetry parallel to the x-axis.
 "Sideways" Parabola Vertex (0,0) "Sideways" Parabola Vertex (0,0)
(axis of symmetry parallel to x-axis)
Conic Forms of Parabola Equations:
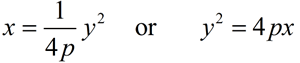
with the vertex at (0,0),
focus at (p, 0), and directrix x = -p
|
We will now be examining the coefficient of y², instead of x². In the example at the right, the coefficient of y² is 1, so 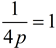 , making p = ¼. , making p = ¼.
The vertex is (0,0), the focus is (¼,0), and the directrix is x = -¼. |
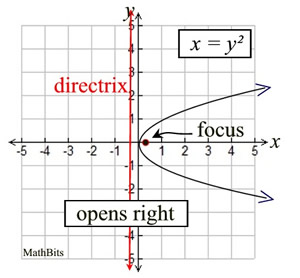 For parabolas opening to the right or
For parabolas opening to the right or
to the left, the y-variable is being
squared (instead of the x² we are
used to seeing for parabolas).
|
 "Sideways" Parabolas Vertex (h,k) "Sideways" Parabolas Vertex (h,k)
(axis of symmetry parallel to x-axis)
Conic Form of Parabola Equation:
(y - k)2 = 4p(x - h)
with the vertex at (h, k), the focus
at (h+p, k) and the directrix
x = h - p |
Sideways Equation in Standard Vertex Form:
x = a(y - k)2 + h
with the vertex at (h, k). |
Since the example at the right is a translation of
the previous graph, the relationship between the parabola and its focus and directrix remains the same.
In the example at the right,
(y - 1)2 = 4(¼) (x - (-2))
(y - 1)2 = x + 2
The vertex is (-2,1), the focus is (-1¾,1)
and the directrix is y = -2¼. |
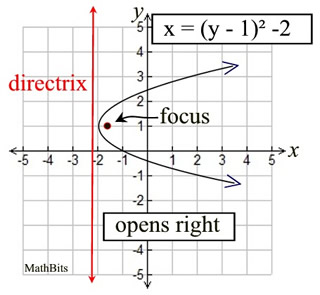 Notice that parabolas that open right
Notice that parabolas that open right
or left, are NOT functions. They fail
the vertical line test for functions.
These parabolas are considered relations.
The Standard "Vertex Form"
and the Conic Form are the same:
VERTEX FORM: x = (y - 1)² - 2
CONIC FORM: (y - 1)² = x + 2 |
S u m m i n g U p: (p is distance from vertex to focus)
| Vertical Parabola (up/down) |
| Vertex (0,0): |
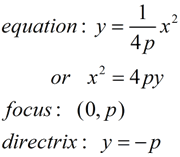 |
| Vertex (h,k): |
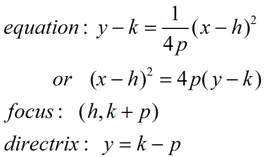 |
|
| Horizontal Parabola (left-right) |
| Vertex (0,0): |
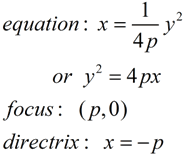 |
| Vertex (h,k): |
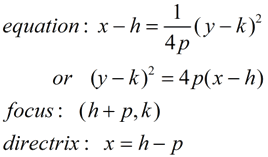 |
|
Deriving the Conic Parabola Equation (vertical): |
 Given x2 = 16y, state whether the parabola opens upward, downward, right or left, and state the coordinates of the focus. Given x2 = 16y, state whether the parabola opens upward, downward, right or left, and state the coordinates of the focus.
ANSWER:
Form: x2 = 4py
4p = 16
p = 4
The focal length is 4.
|
Since this "form" squares x, and the value of 4p is positive, the parabola opens upward.
This form of parabola has its vertex at the origin, (0,0).
The focal length (distance from vertex to focus) is 4 units.
The focus is located at (0,4). |
 Given the parabola, (x - 3)2 = -8(y - 2), state whether the parabola opens upward, downward, right or left, and state the coordinates of the vertex, the focus, and the equation of the directrix. Given the parabola, (x - 3)2 = -8(y - 2), state whether the parabola opens upward, downward, right or left, and state the coordinates of the vertex, the focus, and the equation of the directrix.
ANSWER:
Form: (x - h)2 = 4p(y - k)
Vertex: (h,k) = (3,2)
4p = 8
p = 2
The focal length is 2.
|
Since this "form" squares x, and the value of 4p is negative, the parabola opens downward.
This form of parabola has its vertex at (h,k) = (3,2).
The focal length (distance from vertex to focus) is 2 units.
The focus is located at (3,0).
The directrix
is y = 4. |
 Write the equation of a parabola with a vertex at the origin and a focus of (0,-3). Write the equation of a parabola with a vertex at the origin and a focus of (0,-3).
ANSWER: Make a sketch. 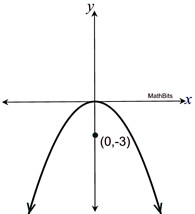 |
Remember that the parabola opens "around" the focus.
Vertex: (0,0) and Focus: (0,-3)
Focal length p = 3. Opening downward means negative.
Form of Equation: x2 = 4py
EQUATION:
x2 = 4(-3)y
x2 = -12y
|
 Find the focus and directrix of the parabola whose equation Find the focus and directrix of the parabola whose equation
is x2 - 6x + 3y + 18 = 0.
| |
ANSWER: You need to complete the square so the vertex, focus and directrix information will be visible.
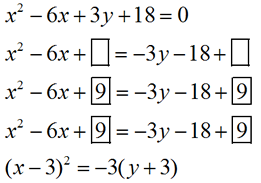 |
|

• The vertex is (3,-3).
• The x-squared term indicates the parabola opens upward or downward.
• The negative value indicates the parabola opens downward.
• The focal length, p, is: 4p = 3;
p = ¾
• The focus is at (3, -3¾)
• The directrix is y = -2¼ |
 Write the equation of a parabola whose focus (-2,1) and whose directrix is x = -6. Write the equation of a parabola whose focus (-2,1) and whose directrix is x = -6.
ANSWER: Make a sketch. 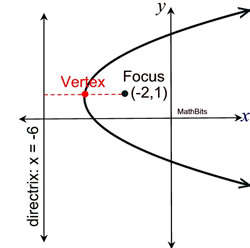 |
Remember that the parabola opens "around" the focus, and the vertex is halfway between the focus and the directrix.
• Vertex: (-4,1) = (h,k)
• Opens to the right (around the focus)
• Focal length, p = 2
• Form of Equation: (y - k)2 = 4p(x - h)
EQUATION:
(y - 1)2 = 4(2)(x - (-4))
(y - 1)2 = 8(x + 4)
|
|