|
Parabolas are relations with one-variable squared (of the second degree).
y = x2
Many of the parabolas we have investigated are also functions.
The design of these parabolas always opens upward or downward, which guarantees that they pass the vertical line test for functions. These parabola functions are also "quadratic" functions.
But what happens if we turn a parabola on its side
so it opens to the right or to the left?
Or, what happens if we square both the x-variable and the y-variable?
|
 |
These new shapes are "relations", but they will not, however, pass the vertical line test to be functions. These new shapes will satisfy the definition of the term "quadratic", and are referred to as " quadratic relations".
Let's take a quick look at a couple of quadratic relations.
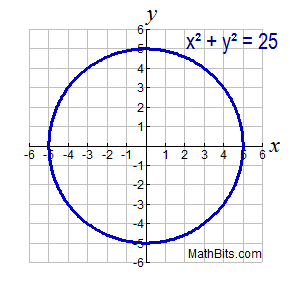
| Quadratic Relation: x2 + y2 = 25 (a circle) |
A quadratic relation containing the square of both the x-variable and the y-variable (with their coefficients being one, or the same value) is a circle. There are two formulas that are commonly used when graphing circles.
 Center at the origin: Center at the origin: |
x2 + y2 = r2 where the center of the circle is the origin, (0,0), and the radius is r.
The equation x2 + y2 = 25 is graphed at the right. The graph is a circle with its center at the origin, and its radius of 5 (the square root of 25). Notice that the coefficients of both x2 and y2 terms are one. Should these coefficients not be the same value, you will no longer have a circle.
|
|
 Center not at the origin: Center not at the origin: |
(x - h)2 + (y - k)2 = r2 where the center of the circle is the point (h,k), and the radius is r.
It is important to note that the "h" and "k" are subtracted from the x and y variables.
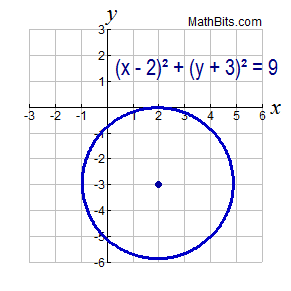
The equation (x - 2)2 + (y + 3)2 = 9 is graphed at the right. The graph is a circle with its center at the point (2,-3), and its radius of 3 (the square root of 9). You need to view this equation as being
(x - 2)2 + (y - (-3))2 = 9
so you can see that h = 2 and k = -3. |
 |
For help graphing circles on your graphing calculuator,
follow the link at the right. |
|
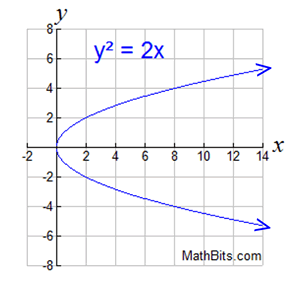
| Quadratic Relation: y2 = 2x (a sideways parabola) |
NOTE: This example is listed for your information only.
Parabolas that open to the left or right have the square on the y-variable, instead of the x-variable.
You can see from the graph that the relation is not a function. It does not pass the vertical line test for functions.
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|